회귀추론을 위한 데이터분석을 하려면 데이터 구조가 중요함
seletion bias를 효과적으로 통제하는 design할 수 있음
Data Structure
1. Cross-sectional data
특정 한 시점에서 여러 unit을 포함함
suvey로 모으면 대표적임!
2. Time-series data
시간에 따라서 변화를 관찰함
주식가격 추이, 국가에서 gdp 추이
3. Panel(longitudinal) data
두 가지를 모두 합친 데이터
여러 유닛에 대해서 시간에 걸쳐서 반복적으로 관찰할 수 잇는 경우
이것이 동일한 유닛에 대해서 시간에 대해서도 모두 관찰할 수 있으면 가능해야 함
추적이 불가능하면 여러 섹션의 크로스섹션을 모아놨다고 해서 panel 은 아
fixed effect를 활용하는 데 제한이 있음
특성이 다르기 때문에 잘 알아두기~

Recall How to Remove the Selection Bias
데이터 구조를 이해하는 것이 중요함
인과추론을 방해하는 최대의 적이 Selction Bias
즉, T가 없는 상황에서 T그룹과 Control 그룹간의 Sysmenic한
비교 가능한 control그룹을 통해서 t그룹에 대 counterfactual을 수정하하는 것임
그래서 selection bias를 야기하는 요인을 Confounder이라고 함
인과추론에 대한 데이터 구조를 이해하는 데 있어서
시간에 따라 변하지 않은 time-invariant
인과추론은 yes or no라는 답이 없고
데이터 특성을 고려했을 때 인과추론의 가정을 얼마나 믿을만한지
데이터 구조에 따라서 인과추론 과정이 어떻게 완화될 수 있는지
신뢰성있는 분석을 할 수 있는지 설명할 것임!!!

Data Structure from the Counterfactual Perspective
1. Time series
만약에 타임시리즈 데이터에서 t이전에 데이터가 없다면?
모두 t 이후에서만 관찰할 수 있다면?
어떤 방식으로는 t 이전을 추정해야 함
but 없으면 아예 인과추론이 불가능한 상태임
-> 그래서 t 전의 데이터가 존재해야 함
과거의 outcome뿐만 아니라 time trend도 추가해야 함
가정에서 벗어난 과정을 treatment 어쩌구임^~~
counterfacual를 추론하는 인과추론의 관점에서는
time series는 control그룹이 없다는 것이 가장 치명적임
seanal effect가 있거나 어떤 가정을 할 수 있음 but 확인을 할 수 없음
time에 의한, Treatment에 의한 변화인지 구분하는 것이 없고 한계가 존재함
인과관계를 추론하는 것이 주된 목적이라면 untretment unit 꼭 찾아야 함

2. Cross-sectional data
Control group을 찾을 수 있는 가장 간단한 데이터 구조
특정시점에 treated outcome에 대한 countfactual에 대해서 treated outcome을 활용하게
결국 control group에서 outcome을 가지고 만약 tretment 그룹에서 treated가 없었다면 있었을 counterfactual 을 추론하는 것이 가능하려면 control 그룹이 모든 측면에서 비교가능해야 함
t를 제외하고!!
counterfacual를 추론하기 위해서 시간에 따라서 변하는 요인, 변하지 않은 요인을 모든 측면에서 비교 가능해야 됨
무작위 실험으로 구분하면 전부 반반으로 구분함
쉽게 가정을 만족할 수 있음
cross라고 인과추론이 불간으한 것이 아님
observation에서는 이러한 가정을 만족하기 힘듦
confounder에 대한 변수를 최대한 많이 모아서 regression에서 cau variable하는 게 좋음
차이를 설명하는 모든 controvariale을 구하기 쉽지 않음

3. Panel data
fixed effect의 역할이 있음!
t 유닛과 unt의 유닛이 있는데 반복적으로 관찰이 가능하면 -> fixed effect 관찰 가능
fixed effect : 각 유닛에 대해서 1, 0으로 나타내는 더미 베리어블임
그래서 3개의 유닛이 있으면 -> 3개의 더미 베리어블을 만들 수 있음
unit A 에 대한 더미 베리어블 데이터 1 나머지는 0
동일하게 unit B, C가 있음
각 유닛에 대한 더미 베리어블을 다 포함하면 각 유닛에서 시간에 따라 변하지 않은 모든 특성들을 반영하는 통제변수역할을 함!
confounder들을 명시적으로 통제할 수 있음
각 유닛의 시간에 따라 변하지 않은 모든 요인들을 통제할 수 있는 또다른 control variable의 역할을 함
시간에 대해 비교 가능한 어쩌꾸..
인과추론이 가능해짐..
panel data
충족하는 과정이 완화됨
fix effect로 다 통제됨
만약 여기서 time-varying confounder를 완화하면 더 쉽게 가능함
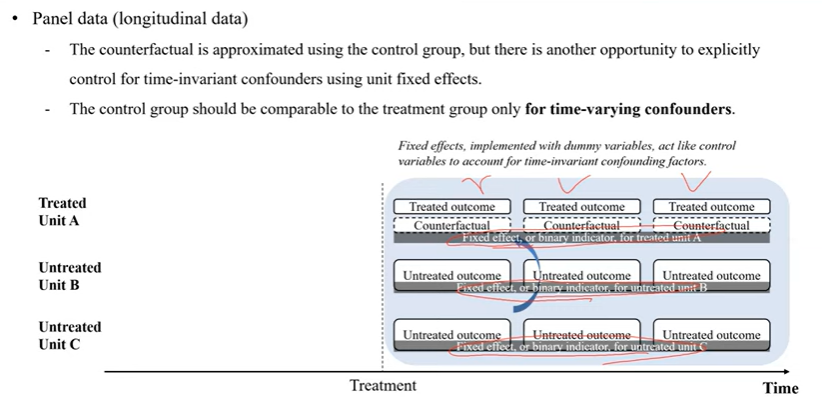
패널데이터에서 T전후의 모든 데이터 구할 수 있으면
한 번의 Chance가 더 있음
시간에 따라 변하는 confounder가 있음
그러한 차이는 t가 없을 때도 비슷한 차이가 존재함
물론 t 이전에 어떤 차이와 t있는 후의 차이는 같지 않음
t가 없을 때에도 시간에 따라 변할 수 있기 때문 - time varying이기 때문에
만약 차이가 시간에 따라 시간의 추세에 변화만 있다면
이 차이를 통해서 time varying confounder을 명시적으로 추정하고 추론할 수 있음
time trend만 변화가능하면 비교가 가능함
인과추론의 과정이 어떻게 완화될 수 있는지 비교분석 해보니까
모두 관찰 가능한 인과추론에 있어서 유리함!!

Fixed-Effects Model Enables Within-Group Comparsion
그런데 fixed effect에서 이상한 부분이 있음
지금처럼 t이후에만 관찰한다면 fixed effect만 넣으면 분석 자체가 불가능함
시간들마다 변호하하지 않은 것을 전부 통제함
unit a, b, c에 대한
Treatment unit a에 대해서는 variable이 시간에 따라 변하지 않을 것임
시간에 따라 변하지 않기 때무네 fixed effect에 전부 흡수되어서 추정이 불간으함
함께 구하려면 TREATE그룹 1인지 0인지가 아니라 Fixed effect가 100 흡수되지 않고 남은 부분이 있어야 분석이 가능
fixed effect를 통해서 시간에 따라 변하지 않은 모든 unit을 통제하면
-> 결국 시간에 따라 변화하는 variancien을 알 수 있음
unit a, b, c 내에서의 변화를 비교할 수 있고
평균값을 통해서 전체를 구할 수 있음
특정 그룹끼리 묶어서 matchingd이랑 비슷한 원리로 작동함!
즉, within-group0 comparsion이 중요함
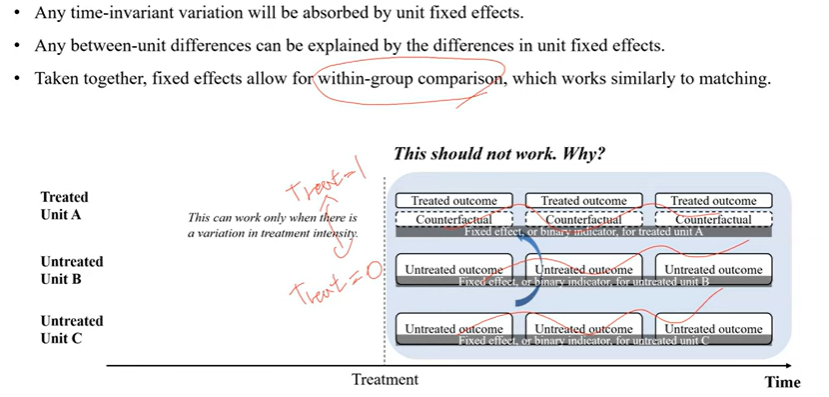
treated unit 내에서는
treatment 전 후가 있기 때문에 이에 대한 차이를 분석함
-> treatment effect를 추정할 수 있
unit b는 처음부터 끝까지 전부 treatment를 받지 않음
BUT treatment effect 어떻게 추정??
IF 이게 제대로 분석될 수 없다면 Untreated unit은 인과추론에 전혀 도움이 되지 않음 ㅡㅡ....
이 역할을 whithn group이 아니라 untreted와 treated 차이를 통해서 구별하는 것임
이 상황에선 어떻게 비교가 가능할까요??
이를 이해해야 fixed effect의 중요성을 알 수 있음
treatement 전제
treatment와 untreatment의 차이를 만들어 주는 데에는 time fixed effect임!!!!
각 시간대 별로 공통된 효과들이 흡수가 됨
같은 시간대별로 whithn time 이걸 가능하게 함
이걸 대비해서 treatment의 효과 발라낼 수 잇음
이런 이유로 panel data 분석을 할 때 time effect도 넣어야 하고
이를 two-way fixed-effect(TWFE) model!
다들 쓰니까 이거를 쓴다~라고 하는 것도 좋지만
역할이 명확하게 무엇인지 알고 인과추론에서 왜 중요한지 깊은 이해를 할 수 있음!!

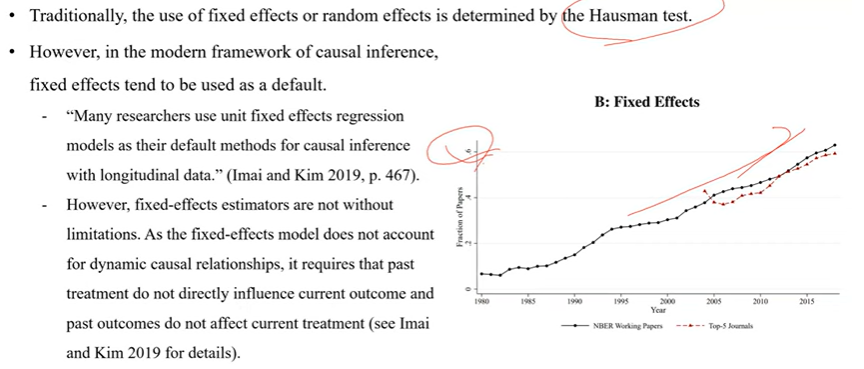
Fixed-Effects Model is the Primary Workhores for Panel Data
전통적으로 fixed effect 나 random effect를 사용할지 결정할 때 Hausman test(하우스먼 테스트)를 자주 사용
BUT 강의자는 이를 많이 비판함.... 그래서 디테일하게 할것임
인과추론 관점으로는 이 테스트는 너무 교과서적인 테스트도
최근 논문에서는 거의 없을 것임
현실적으로 인과추론에서는 Fixed effect를 사용하는 것이 디폴트임!
WHY?
Random effects는 confounder를 제대로 설명하지 못하고 counterfactual를 추정하는 것을 이는 못함 ㅡㅡ
표는 경제학 논문에서 fixed effect는 60%를 쓰고 패널 데이터에서는 거의 다 이 effect를 사용함 !!
한계점도 많지만 이를 대안으로 random effect로 돌아가는 것이 아님 ㅋㅋ
한계점을 극복하기 위한 variaicien이 존재함
random effect를 반드시 써야하는 상황이면 justification을 분명하게 제시해야 함
인과추론의 흐름을 자인하는 꼴이 됨 절대 하우스먼 테스트 xxxxxxxxxx
가장 기본, 핵심되는 도구다잉!!
Clustered Standard Errors in Panel Data Analysis
Common practices으로는~~
i.i.d (아이 아이 디)
동일한 유닛을 반복적으로 관찰함
시간이 흐르더라도 비슷한 요인을 공유함
그들의 outcome은 correlation이 있고
설명 불가능한 factor들도 시간이 변한다고 해도 서로 연관성이 높을 수밖에 없음
즉, panel data는 데이터 특성상 i.i.d 를 위배하게 될 확률이 높음
그래도 각 unit별로 correlation이 있을 수 있다고 허용하는 것이 일반적인 접근임
주로 robust SE랑은 다른 개념임
패널UNIT이 적으면 Efficient한다고 하지 않다고 함
대부분 관행은 50개 이하면 Cluster-bootstrapped standard error를 사용함

'Causal Inference' 카테고리의 다른 글
| Week 3-1 인과추론을 위한 회귀분석의 역할 (0) | 2024.01.18 |
|---|---|
| Week 2-4 실험/준실험 접근법의 한계 (1) | 2024.01.16 |
| Week 2-3 인과추론의 기준점 : 무작위 실험 (0) | 2024.01.16 |
| Week 2-2 잠재적결과 프레임워크의 가정 (0) | 2024.01.15 |
| Week 2-1 잠재적결과 프레임워크 (1) | 2024.01.14 |